Стандартизация
В табл. 7 представлены результаты обследования двух групп населения, которые должны сравниваться на частоту заболевания. Такое сравнение можно делать на основе двух грубых коэффициентов заболеваемости — 0,015 в год и 0,023 в год соответственно. Возрастное распределение населения этих двух групп, однако, различно. Группа с более высоким грубым коэффициентом заболеваемости имеет также большую долю людей пожилого возраста. Возрастное распределение могло бы объяснить более высокий грубый коэффициент заболеваемости в старшей группе населения.
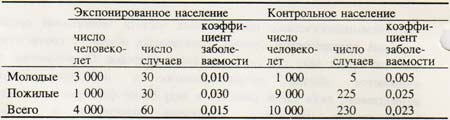
Таблица 7. Число человеко-лет и число случаев заболевания в экспонированной и контрольной группах населения
Одним из способов повышения обоснованности сравнения является проведение так называемой стандартизации. Для понимания этого приема допустим, что грубый коэффициент чего-либо является взвешенным средним значением стратифицированных коэффициентов с весом, пропорциональным числу лиц или человеко-лет в каждой страте. Для представленной в таблице экспонированной группы населения, например, грубый коэффициент заболеваемости равен
(3000 / 4000) * 0,010 + (1000 / 4000) * 0,030 = 0,015.
Для стандартизации по возрасту делается перерасчет. Вычисляют, чему были бы равны грубые коэффициенты, если бы возрастное распределение обеих группах населения было бы аналогично возрастному распределению в стандартной группе. Предположим, экспонированная и контрольная группы населения сливаются с образованием стандартной группы; тогда в стандартной группе будет 4000 / 14000 молодых и 10000 / 14000 пожилых. Стандартизованные коэффициенты заболеваемости составят
(4000 / 14000) * 0,010 + (10000 / 14000) * 0,030 = 0,024
и
(4000 / 14000) * 0,005 + (10000 / 14000) * 0,025 = 0,019.
Разница или отношение этих стандартизованных коэффициентов заболеваемости может использоваться для проведения абсолютного или относительного сравнения. Отношение стандартизованных коэффициентов заболеваемости составляет в данном случае 0,024 / 0,019 — 1,26.
Недостатком метода стандартизации является его зависимость от выбора стандартного населения. В принципе, стандартное население должно отражать распределение признака, для которого оценивается эффект воздействия. В данном примере выбор другого стандартного населения привел бы к другому значению стандартизованного коэффициента. Описанный метод стандартизации называется прямой стандартизацией.
В табл. 8 представлена обычная ситуация. По двум группам приведены почти такие же данные, что и в табл. 7, за исключением информации о распределении случаев по возрасту для экспонированной группы. Отсутствие таких данных объясняется обычно тем, что число случаев слишком мало для осуществления какого-либо значащего деления их на возрастные группы.

Таблица 8. Число человеко-лет и число случаев заболевания в экспонированной и контрольной группах населения
В таких ситуациях сравнение часто производится между наблюдаемым числом случаев О (англ. observed) и ожидаемым числом случаев Е (англ. expected) в экспонированной группе населения. В данном случае О = 60. Ожидаемое число есть число случаев, которые произошли бы в экспонированной группе населения, если бы все повозрастные коэффициенты заболеваемости для экспонированного населения были бы такими же, как для контрольного. В данном примере мы имеем
Е = 3000 * 0,005 + 1000 * 0,025 = 40.
Как наблюдаемое, так и ожидаемое число случаев зависит от возрастного распределения экспонированной группы населения. Наблюдаемое число случаев, таким образом, зависит от коэффициентов заболеваемости экспонированного населения, а ожидаемое — контрольной группы. Отношение наблюдаемого числа случаев к ожидаемому эквивалентно, следовательно, стандартизованному относительному сравнению коэффициентов заболеваемости в экспонированной и контрольной группах населения, при использовании экспонированной группы как стандартной. Такой метод учитывания различий в возрастном распределении называется косвенной стандартизацией, но должен рассматриваться как разновидность вышеописанного прямого метода стандартизации. Отношение наблюдаемого числа случаев к ожидаемому часто выражается в процентах и называется стандартизованным отношением заболеваемости SIR (англ. standardized incidence ratio) или — при анализе смертности — стандартизованным отношением смертности SMR (англ. standardized mortality ratio). В данном примере мы имеем
SIR = (60 / 40) * 100 — 150.
Похожие статьи:
Примите к сведению
Информация на этом сайте представлена в справочных и образовательных целях и не должна быть использована как инструкция по лечению. В любых случаях необходимо консультироваться у врача.