Показатели сравнения частоты заболеваний

По сравнению с исследованиями, в которых просто измеряется частота заболевания в одной группе, в исследованиях связи между экспозицией и заболеванием сравнивают частоту заболевания у лиц с разным уровнем экспозиции. Чаще всего используется отношение коэффициентов, или относительный риск, определяемый как отношение коэффициентов заболеваемости у экспонированных и неэкспонированных. Может также использоваться отношение кумулятивных коэффициентов заболеваемости для экспонированной и неэкспонированной групп. Результат сравнения частоты заболевания не обязательно должен быть выражен отношением: целесообразно также оценить его разностью показателей частоты для экспонированной и неэкспонированной групп населения. При контроле систематических ошибок, любой сравнительный показатель частоты заболевания в группах с различными уровнями экспозиции можно считать показателем эффекта.

Как и простые показатели частоты, показатели эффекта должны представляться вместе с оценкой их точности. И здесь точность наилучшим образом характеризуется величиной доверительного интервала.

Вероятность того, что истинное значение показателя соответствует некоторой точке в пределах доверительного интервала, изменяется на протяжении интервала: вероятность существования такой точки постепенно снижается по мере приближения к его границам. Соответственно, на пороге доверительного интервала не происходит резкого падения вероятности. Поэтому нецелесообразно уделять слишком большое внимание точному расположению границ доверительного интервала. Неважно, включается или не включается в него отдельное значение. Иногда для интерпретации полученных результатов существенно определить, включается или не включается в доверительный интервал конкретное значение, соответствующее отсутствию связи между экспозицией и заболеванием. Такое значение составит единицу для относительного риска и отношения шансов и нуль для показателей разности. Интерпретация будет равнозначной критерию значимости гипотезы об отсутствии связи. Поскольку оценка существенности различия показателей менее информативна, чем доверительные интервалы, и легко поддается неверной интерпретации, мы настоятельно рекомендуем пользоваться для оценки точности эпидемиологических данных не критериями значимости, а доверительными интервалами. Более того, мы не рекомендовали бы использование доверительных интервалов просто для определения того, включена ли в интервал величина отсутствия связи, — т.е., использовать доверительный интервал как эквивалент критериев значимости. Дальнейшее обсуждение интерпретации доверительных интервалов и критериев значимости читатель найдет дополнительно.

Мы покажем расчет доверительного интервала для относительного риска в некоторых стандартных эпидемиологических ситуациях. Описание ситуаций, при которых используются показатели разности, следует искать в специальной литературе.

Если число наблюдений достаточно велико, чтобы воспользоваться нормальным распределением, общую формулу 95%-ного доверительного интервала для относительного риска можно рассчитать так:

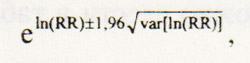
где е — основание натурального логарифма, приблизительно равное 2,718, а ln — логарифмическая функция по основанию е. натуральный логарифм. Экспонента е в формуле представляет собой выражение того же рода, что использовалось в предыдущем разделе при расчете доверительных интервалов для описательных эпидемиологических показателей. Оно начинается с наблюдаемого числа, в данном случае ln(RR) (см. ниже), к которому прибавляется или от которого отнимается умноженный на 1,96 квадратный корень дисперсии var рассчитываемого числа. Общая формула расчета доверительного интервала для RR опирается на нормальное распределение. Конкретные варианты формулы отличаются только расчетом дисперсии, соответствующим типу конкретного исследования. Включение в формулу постоянной е и натурального логарифма обусловлено крайней асимметричностью распределения возможных значений относительного риска, который не может быть ниже нуля, но не имеет верхнего предела. Такая асимметричность ограничивает применимость нормального распределения, которое является симметричным. Логарифмирование делает распределение значений более симметричным, ограничивая длинный «хвост» больших чисел и вытягивая значение от 0 до 1 в сторону минус бесконечности. Приведенная формула устанавливает симметричные границы доверительного интервала в логарифмическом масштабе, преобразуя их затем в первоначальный масштаб путем потенцирования. Ниже мы приводим конкретные формулы вместе с примерами для некоторых стандартных эпидемиологических ситуаций.

Похожие статьи:

Примите к сведению

Информация на этом сайте представлена в справочных и образовательных целях и не должна быть использована как инструкция по лечению. В любых случаях необходимо консультироваться у врача.